ML Explanations
UPDATED: 2021-09-14
This blog post contains concise explanations for various concepts and ideas in Machine Learning that I found useful.
1) Basic Concepts/Techniques
a) Precision, recall, F1
In fraud detection, the precision of 70% means that the detector is correct only 70% of the time. The recall of 95% means that it can detect 95% of the frauds. For this kind of detection, we prefer the detector with high recall to the one with high precision and low recall.
The F1 score is the metric that combines precision and recall. It gives more weight to the lower value.
\[P = \frac { TP } { TP + FP } \\ R = \frac { TP } { TP + FN } \\ F1 = \frac { 2 } { \frac { 1 } { P } + \frac { 1 } { R } } = \frac { TP } { TP + \frac { FP + FN } { 2 } }\]b) Simple Approach for Document Similarity
Given two documents \(D_1 = [w^1_1, w^1_2, ..., w^1_n]\) and \(D_2 = [w^2_1, w^2_2, ..., w^2_m]\), their similarity can be calculated as the average of all the cosine similarity scores \(cos(w^1_i, w^2_j)\), where \(w^1_i \in D_1, w^2_j \in D_2\):
\[sim(D_1, D_2) = \frac{1}{n*m}\sum^{n}_{i=1}\sum^{m}_{j=1}{v(w^1_i) \cdot v(w^2_j)}\]That is equivalent to measuring the cosine similarity scores between two average vectors \(v(D_1)\) and \(v(D_2)\):
\[sim(D_1, D_2) = v(D_1) \cdot v(D_2) = \frac{1}{n}\sum^{n}_{i=1}{v(w^1_i)} \cdot \frac{1}{m}\sum^{m}_{j=1}{v(w^2_j)}\]Here, we assume that word’s embedding vectors \(v(w)\) are already normalized to have unit lengths.
c) Relationship Between Euclidean Distances and Cosine Similarity Scores
Given two vectors \(v_1\) and \(v_2\) having unit lengths, their Euclidean distance and cosine similarity score are related as follows:
\[{\lVert v_1 - v_2 \rVert}^2 = (v_1 - v_2)^T \cdot (v_1 - v_2) = {\lVert v_1 \rVert}^2 + {\lVert v_2 \rVert}^2 - 2 * {v_1}^T \cdot {v_2} = 2 * (1 - cos(v_1, v_2))\]2) LSTM
Most concise form of LSTM:
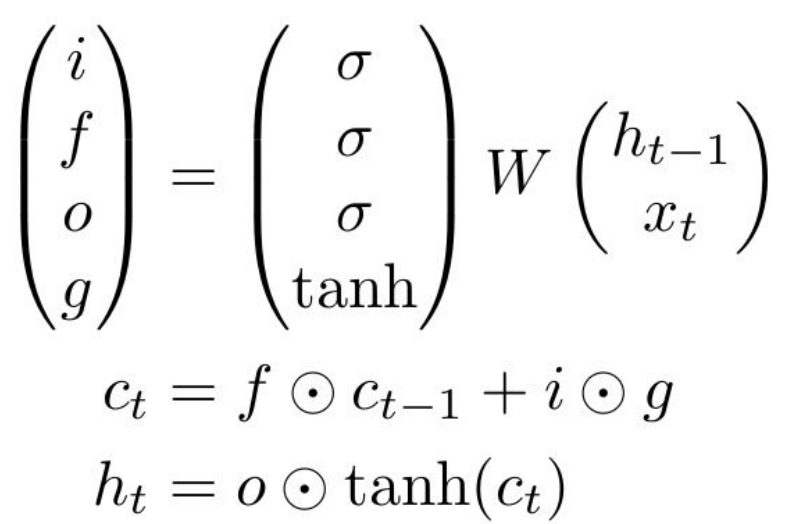 |
 |
Source: Stanford's course CS231n lecture 10
3) CNN
| No padding, no strides | Padding, strides |
 |
 |
Source: Vincent Dumoulin's "Convolution arithmetic"
4) Dot-product attention
With query \(q^{1 x d}\) , keys \(K^{n x d}\) and values \(V^{n x d}\):
\[\begin{align} Attention(q, K, V) = softmax(\frac{qK^T}{\sqrt{d}}) V \end{align}\]The terms are borrowed from information retrieval. For each query q, we retrieve the weighted sum of all values where the weights are determined by how the query matches with corresponding keys. The final result has the shape \((1, d)\).
In dot-product self-attention used in NLP, the query \(q_i\), keys \(K\) and values \(V\) are the linear transformations of word embedding vectors \(x_i^{1xd}\) using the matrix \(W_q\), \(W_k\) and \(W_v\) with the same shape \((d, d)\):
\[q_i = x_i W_q \\ k_j = x_j W_k \\ v_j = x_j W_v\]Source: Peter Bloem's blog post Transformers From Scratch
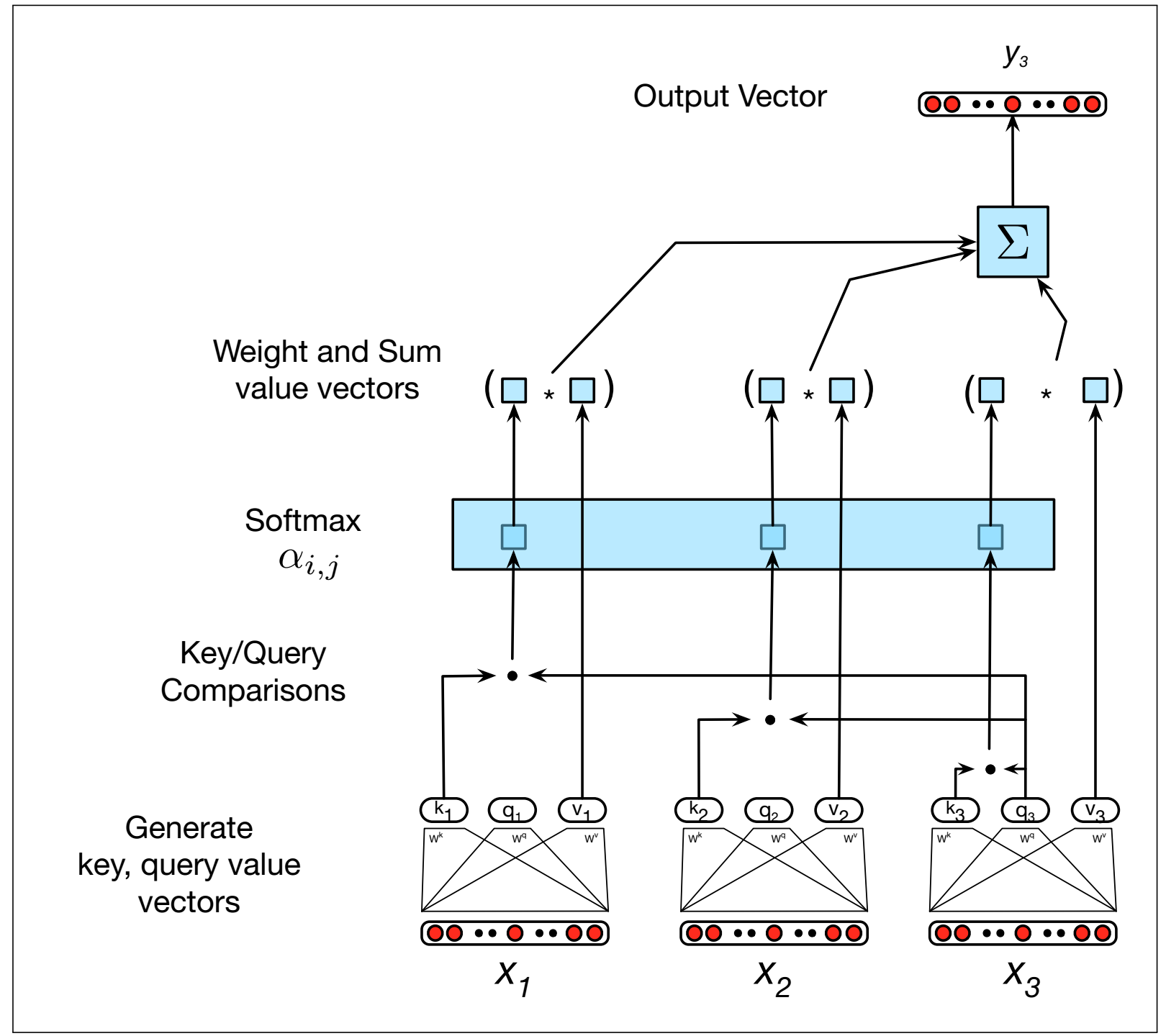 |
Source: Dan Jurafsky and James H. Martin's book "Speech and Language Processing"